PointNet: Deep Learning on Point Sets for 3D classification and Segmentation 논문 리뷰

PointNet 논문은 2017년 CVPR에 게재된 논문입니다. 지금 이 글을 쓰고 있는 시점이 21년이니 4년이나 이전에 나온 논문임에도 불구하고, 그 성능과 간단하면서도 직관적인 구조 때문에 최근 나오는 많은 논문들도 reference로 삼고 있습니다.

3차원 데이터 표현 방법

3D data를 표현하는 방법에는 크게 3가지가 있습니다.

우선 첫 번째로, 2d image에서 화소를 구성하는 가장 기본 단위인 pixel을 3차원으로 확장시켜 만든 정육면체 기본단위 voxel이 있습니다. 그다음 polygon mesh라고 불리는 방법은 작은 삼각형이나 다면체들을 연결하여 더 복잡한 3차원 형상을 표현하는 방법입니다. 3D 게임이나 애니메이션에서 많이 접한 모습일 것입니다. 그리고 마지막으로 point cloud라고 불리는 방법은 3차원 형상의 표면에 점들을 흩뿌려서 3d 입체를 표현하는 방법입니다. 자율주행차에서 사용하는 Lidar센서도 빛을 쏴 점을 찍는 방식이므로 point cloud로 주변을 mapping 한다고 보시면 됩니다. 이렇게 3D 입체를 어떻게 표현하느냐에 따라 딥러닝 모델을 구축하는 방법도 다를 것입니다.

 

오늘 우리가 알아볼 PointNet이라는 논문은 point cloud representation을 그대로 입력받아 classification이나 segmentation 하는 가장 최초의 논문입니다. 그 이전의 논문들은 point cloud의 irregular format 때문에 3D voxel로 transform 하여 3D CNN을 사용하는 등의 방식을 사용하였습니다. 하지만 point cloud를 voxel로 변환하는 과정에서 불필요한 volumeness가 추가되고 3D CNN은 처리해야 할 연산량이 매우 크다는 단점을 가지고 있었습니다. 그럼 Point cloud의 특징은 무엇이며 PointNet은 어떻게 Point cloud를 input으로 받아 처리하였는지 알아보도록 하겠습니다.

 

Point cloud의 특징

1. Unordered.

이미지를 구성하는 pixel들의 array나 3차원 형상에서 voxel들의 array들과는 달리 point cloud는 특정한 순서가 없는 그저 점들의 집합으로 구성되어 있습니다. 예를 들어 N개의 점들이 있다면 이 점들이 네트워크에 들어가는 순서는 총 N!라고 할 수 있습니다. 이때 네트워크는 점들이 들어오는 순서에 상관없이 N! 의 경우에 모두 동일한 결과를 도출해내야 합니다. 즉, 모델이 Permutation Invariance 해야 합니다.

2. Interaction among points.

각 점들은 고립되어 있는 것이 아닌 local neighbor과 함께 상호작용하여 의미 있는 subset을 가집니다. 예를 들어 토끼의 귀에 찍힌 점들은 주변 점들과 함께 모여 토끼의 귀라는 하나의 subset을 형성한다는 뜻입니다. 

3. Invariance under transformations.

Point set으로부터 학습하여 얻어진 representation은 특정 transformation에 invariant 해야 한다는 뜻입니다. 즉, 토끼를 구성하는 point cloud를 rotation하든 translation하든 모델이 이 point cloud가 토끼임을 도출해낼 수 있어야 한다는 것입니다.

 

PointNet의 구조

PointNet Architecture

PointNet은 그 구조가 매우 simple하다는 게 특징입니다. 거의 대부분 fc layer만을 사용하여 훌륭한 성능을 도출했다는 게 눈여겨볼만한 점입니다. input으로 n개 점들의 x, y, z 축 위치(n x 3)를 받아 mlp를 통해 feature vector들을 뽑아냅니다. 모델 중간중간에 보시면 input transform, feature transform이라는 게 나옵니다. input data가 rotation이나 translation에 invarint 하게 하기 위해 canonical space로 변환시키는 역할을 갖고 있습니다. 이 transform은 M. Jaderberg의 Spatial transformer networks라는 논문에서 소개된 T-Net을 좀 더 단순한 방식으로 구현한 것으로, 저자들은 그저 MLP만으로 T-Net이 affine transformation matrix를 예측할 수 있게끔 하였습니다. input point cloud를 PointNet에서 바로 처리하는 것이 아니라 input transform을 통해 canonicalize 하고, 이것을 input points뿐만 아니라 n x 64의 feature vectors에서도 한번 더 canonicalize 해주었습니다. 하지만 feature transform은 64 by 64라는 고차원에서 transformation matrix를 예측해야 하므로 optimization 하는데 어려움이 있을 수밖에 없습니다. 그래서 저자들은 loss에 regularization term을 추가하여 feature transformation matrix가 orthogonal matrix에 유사하게끔 정규화해주었습니다. Orthogonal matrix는 linear transformation의 관점에서 보았을 때, transformation을 하더라도 각 점들 사이의 distance가 유지된다(e.g. rotation, reflection)는 특징을 갖고 있기 때문에 input의 정보를 잃지 않을 수 있습니다.

Regularization term

여러 번의 MLP를 통해 네트워크는 n개의 각 점들에 대한 feature vector들을 학습하게 되고, 결국 n개의 feature vector들이 존재하게 됩니다. 그런데 앞에서 말하였듯 모델은 Permutation Invariance 성질을 가져야 합니다. input의 순서에 상관없이 동일한 결과를 도출하는 함수를 symmetric function이라고 합니다.

Example of a symmetric function

저자들은 permutation invariance를 만족시키기 위해 위의 예시처럼 symmetric function 중 하나인 max함수를 사용하였습니다.

Maxpooling of the PointNet

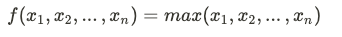
Maxpooling을 거쳐서 나온 feature vector를 global feature라고 부르며 이 벡터는 전체 point set들을 대표하는 representation정보를 가지고 있습니다. Global feature벡터에 한번 더 MLP를 거치게 되면 최종적으로 k개의 클래스에 대한 output scores를 출력 하게 됩니다. 이것이 classification task에서 사용하는 PointNet의 구조입니다.

하지만 Segmentation task는 dense 하게 각 점들에 대한 score를 출력해야 하므로 Classification Network의 중간 부분에서 얻은 n x 64 벡터와 global feature 벡터를 concat 하여 local information과 global information을 함께 사용하게 하였습니다.

 

References

[1] Spatial Transformer Networks arxiv.org/abs/1506.02025

Spatial Transformer Networks

[2] PointPointNet: Deep Learning on Point Sets for 3D Classification and Segmentation arxiv.org/abs/1612.00593

PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation